Divide and Conquer!

The standard algorithm for division may work for you...

DIVIDE

MULTIPLY

SUBTRACT

BRING DOWN

CHECK!

BUT, I have two new strategies that give you a little more freedom with numbers!

You can choose numbers without having to be so precise with each step of the process. 

Suppose that we want to solve the equation 

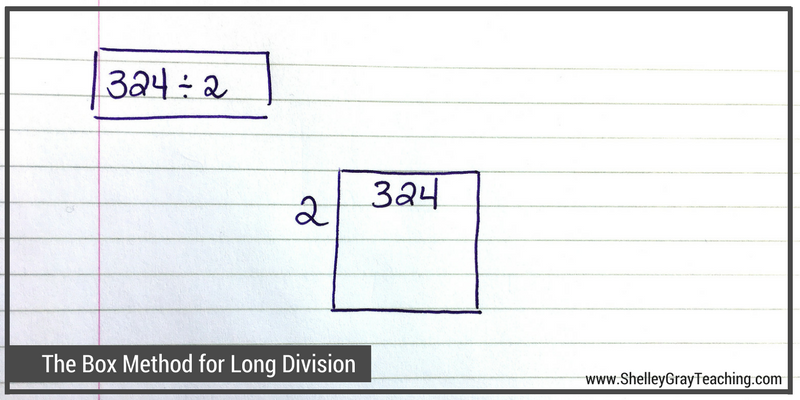
324 ÷ 2

First, draw a box with the dividend on the inside and the divisor on the outside.

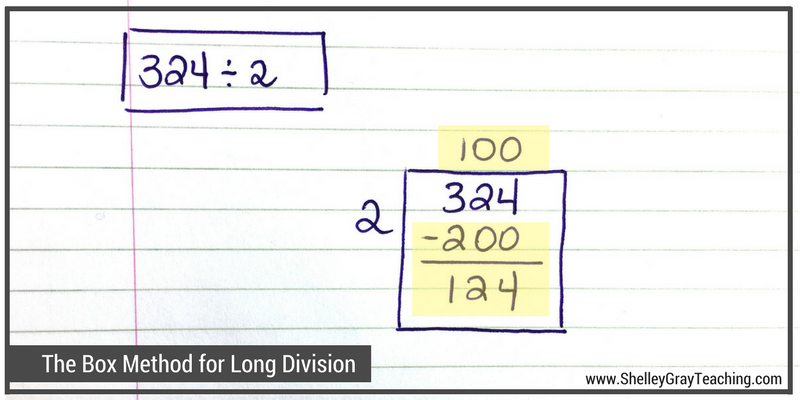
Then, think in multiples to find a number that is close, but does not go over.
Think 10s, 100s, 1000s!

2 x 100 = 200

Subtract and write the answer in the next box.

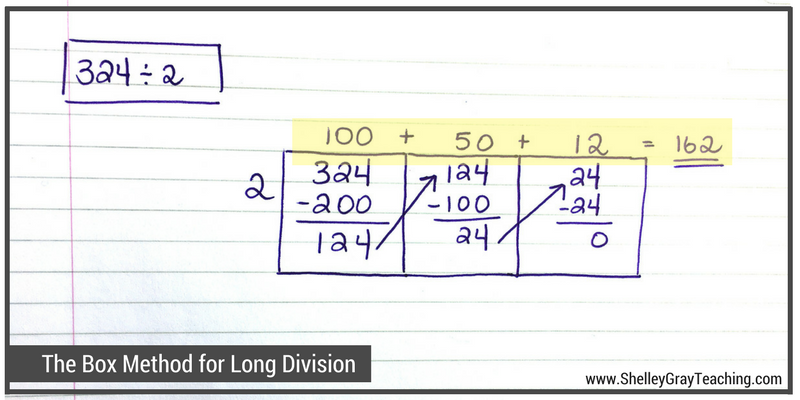
Repeat until you are left with a number that is smaller than the divisor.

Let’s take a look at one more example. 

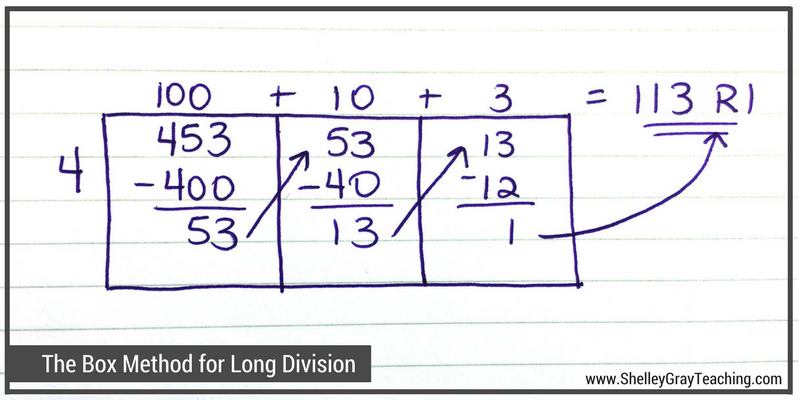
In this example, we will solve 

453 ÷ 4

Draw a box with the dividend on the inside and the divisor on the outside.

Think in multiples to find a number that is close, but does not go over.

Think: 10s, 100s, 1000s!

Think 2s and 5s!

Subtract and write the answer in the next box.

Keep going until you are left with a number that is smaller than the divisor.

When all is said and done, there is a 1 left over...

that's your REMAINDER! 

113 r 1    or     113 1/4

The area model strategy works with 2-digit divisors too! 

Here's an example from page 20 in your Math Activity Book:

Step 1: Think of a few easy X facts for the divisor.

Step 2: Subtract from the dividend an easy multiple of the divisor (e.g. 100x, 10x, 5x, 2x). Record the partial quotient in a column to the right of the problem.

Step 3: Repeat until the dividend has been reduced to zero or the remainder is less than the divisor.

Step 4: Add the partial quotients to find the quotient.

Let’s solve

679 ÷ 5

Click on the images above for a closer look.

Visit Shelly Gray's math website for the videos above and many other helpful math lessons!